February 2009 Archives

Nymegade

By Troy on February 28, 2009 7:42 PM | 4 Comments

A pesar de no entender ninguna lengua viva del planeta azul, exceptuando la suya materna, E. S. Ortigueira es presidenta de la Asociación Mundial de Videntes. Ella se expresa y escribe pulcramente también en nymegade. Para desarrollar su trabajo esto constituye una ventaja considerable. Aunque sólo sus más íntimos lo saben, traductora simultánea se ajusta más a su desempeño profesional que vidente.

El primer mensaje de los seres del océano de agua salada le llegó cuando su padre perdió el empleo en la fábrica. Sólo después de repetirlo fielmente a su madre en voz alta, cayó en la cuenta de que aquello no era gallego.

En estos tiempos de incertidumbre económica ha aumentado el número de tarotistas de la noche a la mañana y cualquiera hace un curso y ya dice que es tarotista. Y esto no puede ser así de ninguna de las maneras, porque podríamos terminar como los informáticos. La profesión, como los bancos, necesita de una mayor regulación y, sobre todo, un colegio profesional oficial que tenga por objetivo el facilitar el progreso continuo de la profesión en relación con las necesidades de la videncia, en particular, y de las empresas y la sociedad, en general.

La crisis ha traído más clientes y ha cambiado su perfil. Más ejecutivos y gente del mundo de los negocios solicitan estos servicios. Hasta noviembre de hace dos años el 83,7% de las consultas estaban relacionadas con el amor, y ahora, el trabajo es la principal preocupación de la mayoría.

Las torres

By Ludwig on February 27, 2009 9:12 PM | 1 Comment

El profeta se volvió al pueblo congregado y dijo: "Aquí podéis ver las torres, derribadas por Dios mismo hace milenios. Aquí Babilonia quiso construir hasta llegar al cielo, y vinieron hombres de todas las naciones para llevar a cabo esta obra de la soberbia humana. Pero cuando estaban a punto de llegar al cielo, mandó Dios unos pájaros de fuego que derribaron las torres, y todos los hombres que las estaban construyendo murieron de una muerte horrible, despeñados desde las alturas."

El pueblo escuchaba con atención, pero miraba alrededor por si acaso: nunca se podía saber qué espíritus rondaban por las viejas ruinas.

Siglos más adelante, el maestro entregaba un cuadro terminado: "Las dos torres de Babel". Aunque los aprendices de su taller copiaban sus naturalezas muertas y mitos clásicos en cadena, asegurándole de sobra el sustento, el maestro había producido este cuadro él solo de principio a fin, desde el lienzo, a los colores, al cuadro finalizado y envuelto, como cuando era joven. Si se sentía conmovido por la historia del ascenso y la caída de la Humanidad, o quería asegurarse fama inmortal de nuevo, no lo compartió con nadie en su taller.

Al salir de palacio, le dio dos monedas de plata a un niño harapiento que iba de la mano de su madre, cuando ella no miraba. Un gesto absurdo de benevolencia. La madre se preguntaría durante semanas de dónde sacó el niño tanto dinero.

El arquitecto se plantó ante los representantes de la Corporación Metropolitana cuando acabaron de curiosear entre las maquetas y los planos, y dijo con voz firme: "Éste no es un proyecto como los demás, ni para mí, ni para ustedes en la Corporación. Creo expresar la opinión de todos los presentes al decir que estas torres representan el orgullo de nuestra ciudad, la promesa que nuestro país le hace al mundo: prosperidad. Prosperidad sin límites, para todos los que quieran trabajar honradamente. Aquí la ciencia y la técnica nos permiten construir lo que nuestros antepasados sólo soñaron."

En su desierto, el profeta ya iba extendiendo la mano hacia el Kalashnikov.

Sin violencia aparatosa

By Troy on February 27, 2009 6:14 PM | No Comments

Roberto Sánchez Colmenarejo se fumó el primer porro, acompañado de su padre, a los once años. A esa edad ya se había calzado al menos doce veces a su vecina Fernanda y lucía mostacho resultón. Casimiro Sánchez Fernández, su padre, era de la opinion que los porros no son malos, lo malo son las sobredosis o bajodosis, las composiciones alteradas fraudulentamente, su prohibición y lo que uno pueda hacer bajo los efectos; pero esto, si es reprobable bajo los efectos, lo es bajo sobriedad también; luego por qué involucrar a los petas en ello.

Ahora RSC tenía o era diecisiete años. No había cotizado nunca a la Seguridad Social a pesar de haber abandonado la educación reglada a los ocho años y generado ingresos para su manutención, Manuela y prole desde entonces.

Su pasión era el júrgol. Le llenaba de alegría y confianza en la justicia cósmica y existencia de un dios bueno el que alguien con menos cerebro (pieza que al parecer nos distingue del resto de primates) que un mosquito ganara más pasta en un año, por pegar patadas a un balón en calzones, que la mayoría de sus congéneres en toda su vida.

El puto menisco frustró su caso. Pero su deep burning inside no murió. Algún chavalín de su barrio (relación filial no necesaria) llegaría y él habría contribuido de algún modo; aunque sólo fuera llevándolos de ocho en ocho en su Toyota Corolla XLI negro a entrenamientos o partidos.

No lo vió coño no lo vió. Los policías locales siempre allí apostados para que los más débiles caigan. Volvían de un entreno y él no había fumado más que cualquier otro día. Se salió un poco de la curva y empotróse sin violencia aparatosa con el vehículo de trabajo de la autoridad. No hubo daños personales y los materiales... vamos no me jodas.

Los capitanes de la industria

By Ludwig on February 23, 2009 3:52 PM | 1 Comment

Cuando vi la pompa que rodeaba la votación del Presidente de los Estados Unidos, se me ocurrió que, como en Francia, allí también tienen un "rey republicano". De hecho, es prácticamente lo mismo que la elección de un rey en la Edad Media: sólo puede proceder de una elite muy restringida, y el cuerpo electoral comprende por un lado a las personas letradas y por otro lado a las personas con intereses económicos fuertes. A los demás no hace falta ya excluirles: tristemente, se excluyen ellos solos.

La ascensión de un rey en sus tiempos no era mucho más que la elección de un cabecilla militar ("Commander-In-Chief"), especialmente entre los pueblos germanos y celtas. Con una duración media del reinado en torno a los diez años, se daba también esa "sana alternancia" que tanto nos alaban, si bien no había retiro dorado para los reyes depuestos. Los celtas, en especial, ejecutaban ritualmente al rey pasado un año. Una alternancia asegurada, y además, un refuerzo de que el rey elegido verdaderamente quiera anteponer las necesidades de la sociedad a las suyas propias. En otras culturas bastaban las constantes guerras y enfermedades, sumadas a la presión genética de la parentela, en forma de envenenamientos y lamentables accidentes.

Llevando la analogía más lejos, los capitanes de la industria son exactamente como los antiguos señores feudales: son factores de poder parcial, que pueden enfrentarse al poder real o incluso ser más poderosos que él. Su poder no proviene de la tierra, como tampoco entonces crecía el poder en los naranjos: su poder es su organización, es decir, su ejército.

Certeros cogotazos

By Troy on February 22, 2009 10:49 AM | 1 Comment

María es toda una mujer de pelo en pecho. Vivía con su mudo amante Rob. Una tarde descubrió a Rob ejerciendo de coprófago a escondidas. Tras saberse observado, Rob no paró en su actividad y se limitó a mirar de reojo mansamente a su hasta entonces amante como no advirtiendo que aquello no era aceptable por nuestra sociedad. María sintió una ira que no conocía. Días después cayó en la cuenta de que esa indignación podía venir de que los amantes se besan en la boca.

Su apetito de venganza empezó a saciarse pronto. Los cinco metros de vestíbulo que le separaban del infractor le dieron para quitarse el cinto. Con su mano derecha agarró con fuerza la hebilla y el otro extremo de su arma de cuero. Rob tenía cara de no saber lo que se le venía encima. Al primer zurriagazo en su lomo, dejó de comer. Al quinto, emitió su primer quejido. How convenient is that! - pensó la agresora. El objeto de mi enojo permanence parado a pesar de mis repetidos latigazos en lomo y costado.

Debería terminar con el castigo. La pena, para ser justa, debe ser proporcional a la ofensa. Ya pero es que estoy disfrutando mucho. Mi vida alcanza raramente estos niveles de entretenimiento. Además presiento mi impunidad. Nadie sabrá nunca de mis acciones. El que Rob sea mudo ayuda. Procuraré no dejarle marcas. Una vez leí un consejo que un imam daba a maridos que no vivieran en sociedades musulmanas. Naranjas en una bolsa no magullan a tu esposa o esposas (hasta cuatro son vistas con buenos ojos por Alá).

Al día siguiente Rob estaba menos cariñoso que de costumbre. Todo fluyó pacíficamente hasta que Rob exigió más atención de la que María estaba dispuesta a concederle. Tres certeros cogotazos le hicieron comprenderlo.

La relación estaba irremediablemente rota. María fue consciente de esto desde el primer momento. ¿Está la violencia justificada en algún caso? La violencia genera más violencia. María ya llegaba a casa después del trabajo con ganas de cascar a Rob, pero primeramente y cada vez, debía encontrar un motivo razonable. Como María era primera y última instancia, todos sus motivos caían en la categoría de sensato.

Rob terminó pagando por todo. Un mal día de trabajo de María. Alguna zorra manipuladora que maltratara a María por envidia. Cualquier cosa. Las humillaciones y vejaciones sufridas por Rob fueron variadas pero finitas en número y días. Fue orinado sobre su cabeza. Restregada su cabeza sobre su mierda en el suelo. Arrojado por una escalera de veinte peldaños. Apaleado. Zarandeado. Lanzado al aire con estación de destino única suelo duro.

Rob temblaba cuando María se le acercaba. Error. Esto excitaba y ponía todavía más cachonda a María. No se puede hablar de sadismo porque la crueldad no era refinada. María era simplemente proterva. Obstinada hasta que dejó de vivir con Rob pero esperando al siguiente. Los resortes están ahí.

Improvisadamente referir oralmente

By Troy on February 21, 2009 11:24 PM | No Comments

Supe por primera vez de Jaime Bayly hace unos meses en youtube en una entrevista televisiva que hacía a FJL. Me cayó bien. Luego apareció otra vez en youtube entrevistado por FSD con motivo de su entonces nuevo libro "El canalla sentimental". Compré el libro, lo leí y compré otros cinco libros suyos. Acabo de terminar de leer el que parece más breve de los cinco si atendemos a sus lomos, "Y de repente, un ángel" (Ydrua). Desde 2005 tiene JB derechos reservados por Ydrua.

La imagen pública de JB es la de un cínico, alguien que muestra desvergüenza en el mentir o en la defensa y práctica de acciones o doctrinas vituperables; alguien impúdico, procaz, obsceno y descarado. Adopta el enfoque de Petronila (Ydrua) cuando dice: "Yo ya estoy vieja y todo me da igual, oiga". No miente porque no manifiesta lo contrario de lo que sabe, cree o piensa. Como relativista, lo que sabe, cree o piensa no está quieto. No busca la verdad (no existe), busca la provocación que lleva al placer, la diversión o el entretenimiento. Vituperables en una sociedad tradicionalista, reaccionaria e intolerante (absolutismo viejo). La impudencia le viene al autor de su falta de imaginación para formar nuevos temas narrativos que no tengan que ver directamente con vivencias personales suyas. Los dos libros suyos que he leído reflejan fielmente su imagen pública, con él como narrador y personaje principal de la acción.

Es peruano como Mario Vargas Llosa y tiene la misma voz, cadencia, musicalidad encantadora de serpientes. Es difícil que alguien capaz de improvisadamente referir oralmente cómo se corta las uñas de los pies de tal modo que deleite al oyente no sea un buen escritor.

Algo del español americano del libro y del otro. JB no se agita con franelas o tejidos finos de lana o algodón, ligeramente cardados por una de sus caras, usados usualmente al parecer para quitar el polvo. Una mucama es una persona que sirve por un salario, y especialmente la que se emplea en el servicio doméstico. Los diarios se hojean y se ojean. El entrevero de coches en Lima es nada comparado con la confusión y desorden de vehículos en Cairo. No sólo en Perú al autobús le llaman colectivo. Las pantuflas son calzados sin orejas ni talón que para mayor comodidad se usan en casa. Nomás es un adverbio de modo que se usa en oraciones exhortativas, generalmente pospuesto, para añadir énfasis a la expresión. Un ejemplo aparece cuando la mucama Mercedes le responde a su patron JB "... vaya nomás a dormir...".

"No se puede generalizar"

By Ludwig on February 19, 2009 6:35 PM | 4 Comments

Una red social en realidad es un grafo matemático, en el que cada miembro se representa como un punto y cada conexión como una línea entre puntos.

Una de las propiedades más conocidas de la red social humana es la que se llama "seis grados de separación". Fue propuesta en los 60 por un profesor de sociología al comprobar que ése era el grado medio de saltos que necesitaba una carta para llegar a su destinatario, partiendo de un primer remitente que no conociera más que el nombre del destinatario. Más tarde se ha demostrado matemáticamente que éste es realmente el grado medio de separación entre dos miembros de la red social humana.

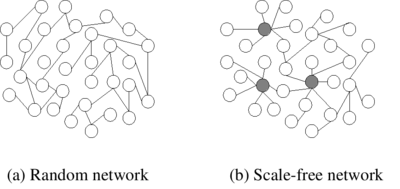
Resulta que esta propiedad, llamada también "efecto de mundo pequeño", proviene de otra más general: la "ausencia de escala". La ausencia de escala se demuestra al comparar el grado medio de conexiones que tiene un miembro de la red, con el grado medio de conexiones que tiene un grupo de miembros de la red... y así hasta considerar la red entera. Para ciertas redes, en las que las conexiones no son ni demasiado numerosas ni demasiado escasas, este grado medio se mantiene constante a lo largo de todas las escalas, desde considerar nodos individuales, a conjuntos de nodos, a considerar la red entera como dos mitades. Es decir, la red parece la misma, sea cual sea el grado de aumento con que la miremos.

La ausencia de escala, a su vez, se origina en la distribución de probabilidades que rige la cantidad de conexiones que tiene cada nodo. Si esta distribución es polinómica, es decir, tiene la famosa "larga cola", entonces la red parece la misma a diferentes escalas. Es decir, si existe una probabilidad bastante mayor que la gaussiana para encontrar nodos con una gran cantidad de conexiones por encima de la media, entonces la red es "un mundo pequeño".

En la imagen b), los nodos grises son los centros de conexiones que permiten alcanzar en seis pasos cualquier punto desde cualquier otro. Estos centros serían infinitamente improbables si las probabilidades fueran gaussianas, como en a). Si ampliáramos la imagen b), encontraríamos una imagen similar, en la que cada nodo blanco sería un grupo de nodos blancos normales y un nodo gris que actúa de centro.

La distribución de conexiones en la sociedad humana sigue entonces una ley con "larga cola", una ley polinómica, también llamada distribución de Pareto... al igual que la distribución de la renta. La renta, o sea el parné, es en realidad un sistema de modelado para representar todas las demás materias que son escasas y necesarias; es decir, que son recursos. Y la economía es el sistema de decisión encargado de gestionar estos recursos.

Dejadme formular entonces una hipótesis algo fuerte: el verdadero y único recurso económico son los contactos. Todos los demás recursos pueden ser substituidos mediante el progreso tecnológico, incluida la tierra.

La otra hipótesis interesante que podemos formular es que no sólo podemos generalizar sobre las sociedades humanas, sino que las generalizaciones son siempre exactamente ciertas, dentro de una variación estadística. La generalización es tomar a una parte como descripción del todo. Pero eso es precisamente la ausencia de escala de la sociedad humana: sus partes son iguales, en esencia, que el todo.

Las relaciones laborales en una oficina reflejan exactamente las relaciones internacionales entre un grupo de Estados, unos con mayores capacidades, otros con menores, sus filias y sus fobias.

Las relaciones en el patio de un colegio representan exactamente las relaciones entre diferentes partidos políticos, entre facciones dentro de una empresa, entre conglomerados industriales...

Los estereotipos nacionales tienen "una parte de verdad" porque son correctos. Esto no quiere decir que las sociedades no puedan cambiar, ni que los individuos no se correspondan con su estereotipo (por eso digo "dentro de una variación estadística").

Un ama de casa puede ser mejor Ministro de Economía que el Ministro al cargo, porque su economía familiar es igual que la economía nacional.

Fascinante, ¿no? ¿No parece evidente, al considerarlo?

La alienación

By Ludwig on February 17, 2009 3:16 PM | 2 Comments

"Alienación" es la palabra en castellano que se ha utilizado para traducir "Entfremdung". "Entfremdung", a su vez, es el término que Marx tomó de Hegel para nombrar el alejamiento de sí mismos y del resultado de su trabajo que la sociedad capitalista produce en los trabajadores. (Hegel, por su parte, hablaba del alejamiento que sufre el espíritu racional al habitar en el mundo material).

"Alienación" siempre ha sido una palabra extraña. No creo que nadie la haya visto jamás como otra cosa que un "palabro" usado para designar un concepto oscuro, propio de filósofos alemanes.

A mí me parece que la traducción no es muy afortunada, porque lo que quería decir Hegel, y Marx también, es "enajenación", en el sentido de enajenación de bienes, o expropiación. "Entfremdung", de hecho, es un término jurídico que significa precisamente eso. El sistema capitalista expropia a los trabajadores del producto de su trabajo, porque les da el sueldo que necesitan para sobrevivir, no el valor entero de su trabajo. Así es cómo las empresas arrojan un beneficio para sus accionistas. En este sentido, es un robo.

Además, "enajenación" tiene también el sentido psicológico de la palabra alemana: un enajenado puede significar un loco. El capitalismo, en la descripción de Marx, hace creer al trabajador que debe cooperar en el mecanismo que le perjudica, porque no tiene otra opción. Al trabajar en contra de sus propios intereses, el trabajador está loco desde un punto de vista racional. Desde un punto de vista psicológico, ser sólo una pieza del engranaje productivo produce una ansiedad que se ha reflejado a menudo en el arte del siglo XX.

Lo próximo: redes sociales y termodinámica.

El yomismismo

By Ludwig on February 16, 2009 3:07 PM | 14 Comments

Los yomismistas americanos son un fenómeno que no ha logrado nunca calar en Europa -- a excepción de Austria a nivel académico. Los llamo "yomismistas" porque el término "libertario" ya tiene denominación de origen, y se producen equívocos.

¿Es posible un anarquismo de derechas? Yo creo que sí. La descripción "izquierda-derecha" se queda coja a la hora de explicar porqué anarquistas y comunistas son diferentes, o por qué los liberales ingleses lucharon contra Hitler. Aparte del eje izquierda-derecha, hace falta un eje libertario-autoritario.

fuente: http://www.politicalcompass.org/analysis2

Arriba a la izquierda queda el comunismo, arriba a la derecha el fascismo, abajo a la izquierda el anarquismo y abajo a la derecha el "yomismismo" (en versiones menos radicales, el neoliberalismo).

Mi problema con el yomismismo, aunque no lo vea mal del todo, es que nunca considera que la desigualdad sea una falta de libertad. Una de las ideas más interesantes que encontré en la filosofía de Bakunin - o más bien mística de Bakunin - es que mi libertad no está limitada por la de los demás, sino que se apoya en la de los demás. Una idea algo contraintuitiva, pero a la que merece dar un par de vueltas.

La sociedad (el pacto social de Rousseau) sólo me interesa como individuo porque me permite vivir mejor colaborando en un trabajo especializado que produciendo mi propia comida y vivienda. Me apoyo en el trabajo de los demás para tener más tiempo libre, en el que buscar mis propios objetivos.

Nuestro querido hombre de una sola cita, Isaiah Berlin, nos "enseñó" (como dicen los intelectuales de El País cuando sacan esa cita) que libertad e igualdad son incompatibles, es decir, hay que elegir o la una o la otra -- es una cita muy socorrida cuando hay que sacrificar la libertad por una supuesta seguridad, o hay que sacrificar la igualdad por la libertad de empresa.

Podríamos representar ese pensamiento matemáticamente diciendo que libertad e igualdad son variables ligadas. Por ejemplo, en un círculo.

donde "x" representa por la libertad, "y" la igualdad.

¿Cuál es el radio de ese círculo? ¿Es la "capacidad de organización" de la sociedad? ¿Es la renta per cápita? ¿Puede ampliarse el radio mediante el avance científico y tecnológico? ¿Cuál es el centro del círculo? ¿El "sesgo" político de una sociedad: por ejemplo, el autoritarismo atribuido a los alemanes y el antiautoritarismo de los ingleses?

Deja de meter la cabeza en un cubo cuando las campañas de Tráfico te molestan, coño, y escríbeme en ecuaciones.

Dejadnos solos

By Troy on February 14, 2009 10:59 PM | 6 Comments

Llevo unos meses trabajando en Inglaterra. Ni en Austria, ni en España, ni en Egipto he notado tanto el aliento del estado en mi cogote. Cuanto mayores sean los impuestos que recauda un estado, más intenso puede llegar a ser su aliento. El estado está presente en todos los medios de comunicación de masas (cine, televisión, radio, prensa, paradas de autobús...) lanzando machaconamente consignas que buscan impresionar fuertemente el ánimo. Pongamos dos ejemplos:

El tabaco. Si fumas vas a disfrutar menos tiempo de tus hijos. Si fumas durante el embarazo expones a tu hijo a 4.000 (aquí 4,000) sustancias nocivas que van a hacer que su peso al nacer sea menor y su irritabilidad durante sus primeros años de vida muy superior. Si fumas, tus mascotas se convierten en fumadoras pasivas y acortas su vida en un porcentaje muy alto.

Los accidentes de tráfico. Si incumples las normas de tráfico eres un criminal y la policía te tratara como tal. Dialogo peliculero simulado entre un infractor y la policía donde está le trata como a un trozo de mierda. Una voz de niño relata: cuando se levanta por la mañana, yo estoy allí. Cuando tiene una reunión de trabajo, yo estoy allí. Cuando juega al fútbol con sus amigos, yo estoy allí. Cuando pasea con su mujer, yo estoy allí. Cuando da el beso de buenas noches a su hija, yo estoy allí. Soy el niño que mató hace 7 años por conducir a una velocidad indebida. No me puede olvidar.

Lo que más me llama la atención es no solo su efectismo sino su omnipresencia. No pasa media hora sin que te hayan cascado un mensaje intimidatorio.

Esta intromisión ilegítima en mi vida me llena de ira, indignación y enojo. Tomando palabras prestadas de Chávez (ese gran demócrata bolivariano): "Váyanse al carajo cien veces, estatistas de mierda. Aquí hay un pueblo digno. Aquí estamos los hijos de de la Ilustración. Estamos resueltos a ser libres. Pase lo que pase y nos cueste lo que nos cueste. Ya basta de tanta mierda de ustedes burócratas. Ojalá, enchaala, salamoalekum, más pronto que tarde, los estatistas nos respeten porque nosotros merecemos respeto".

Nunca nombre de coalición humana alguna fue tan bien puesto para llevar a su adhesión inmediata sin entrar en detalles. "Dejadnos solos". El artículo de Grover G. Norquist (presidente de Americanos por la reforma fiscal, http://www.atr.org) la explica en http://www.haciendapub.com/norquist.html

Destacar su descripción de a quién nos enfrentamos "... abogados defensores, grupos que controlan las actividades políticas en las grandes ciudades, líderes sindicales y las dos ramas del movimiento por la dependencia - aquellos que permanecen atrapados en la dependencia y aquellos que ganan 85.000 dólares al año gestionando la dependencia de los anteriores y se aseguran de evitar que consigan empleos y se hagan republicanos. Se les unen totalitarios utópicos de variado pelaje que quieren reorganizar la sociedad por la fuerza e impedir que vistamos cuero o conduzcamos vehículos con tracción en las cuatro ruedas o poseamos grandes cuartos de baño o vivamos de un modo distinto a como ellos consideran adecuado..."

La funesta manía del igualitarismo

By Ludwig on February 12, 2009 1:01 PM | 1 Comment

En un tono entre macrobiótico y catequista, vuelves a cantar las bondades de la democracia realmente existente y del mercado abierto veinticuatro horas. "Un organismo eternamente joven". Qué Mario Vargas Llosa.

Coincidimos totalmente en que la interacción social se basa en las decisiones individuales, y en que esa interacción debe ser libre y flexible. Por mucho que te empeñes en asignarme el papel de bolchevique.

Pero tú no quieres ver el estado de las cosas en muchas partes del mundo, si no en todas: la decisión de la mayoría no cuenta nada. No se nos necesita ni siquiera para ser explotados, como pensaba Marx y sigue pensando la izquierda ortodoxa. Hoy en día, se hace cola para ser explotado. Ante el INEM o en las fronteras de Europa.

Hay razones, más allá de la funesta manía del igualitarismo, para querer cambiar este estado de las cosas. Por ejemplo, la distribución de la renta de Pareto es tremendamente injusta, pero además demuestra que la economía funciona mediante una distribución de Cauchy, no una de Gauss.

La distribución de probablidades de Cauchy tiene una desviación media mucho más larga que la de Gauss. Esto da lugar, por ejemplo, a los efectos de "larga cola" que está en la base del éxito de Amazon y otros proveedores de Internet: existen infinitos nichos que servir en el mercado. El lado negativo es que los modelos matemáticos basados en Cauchy muestran turbulencias mucho mayores que los modelos basados en probabilidades gaussianas, que son los que se usan tradicionalmente en la economía.

Los economistas partidarios del libre mercado sin restricciones subestiman por método el riesgo del mercado. Cuando llegan las turbulencias financieras, son mucho mayores de lo que se consideraría posible según las probabilidades dadas por la curva de Gauss. Si alguien hubiera hecho el cálculo en 2007, apuesto a que la quiebra de Lehman Brothers hubiera sido más improbable que la combustión espontánea de la atmósfera.

La curva de Gauss describe las probabilidades cuando cada suceso no se ve afectado por los sucesos anteriores. Es totalmente correcta para entidades inanimadas, como los átomos, y también para entidades que uno ve como imbéciles que no saben de qué va la cosa, como los consumidores desde el punto de vista de un economista.

La curva de Cauchy, o de Lorentz, es la solución en situaciones donde hay resonancia. Es decir, cada suceso está acoplado al resultado de otros. Como cuando mi comportamiento de consumo no es el de un ciego sordomudo, sino el de alguien que lee las noticias o incluso habla con otros. Y qué decir tiene que no sólo los consumidores, también los empresarios ajustan su comportamiento a previsiones que son a veces empíricas y a veces místicas. Así sí puede suceder que un banco pierda el 95 % de su valor bursátil en un año.

Esta resonancia es lo que tú reconoces en tu descripción ("las decision propias y de tus congéneres"), pero no tienes en absoluto en cuenta. Así, el mundo está en perfecto orden siempre que alguna vez se convoquen elecciones; las estructuras de poder y los estamentos sociales son perfectamente permeables y cambiantes.

En realidad soy partidario de la economía de mercado, pero de mercado real. Si las decisiones de producción están realmente descentralizadas, entonces el igualitarismo no es un deseo, sino una condición previa para la eficiencia del modelo. Lo que tenemos hoy día es una burda parodia de ese ideal. Si un broker de Wall Street decide que hay que hacer cañones, ya puedo comprar mantequilla como un loco, que va a dar igual: será cañones lo que se haga.

No debemos querer la igualdad porque nos parezca más correcta: debemos quererla porque nos beneficia más.

Vehículo motorizado

By Troy on February 11, 2009 10:39 PM | No Comments

Acabo de escuchar la canción de la señorita Spears. No sabía quien la interpretaba a pesar de que aquí la ponen con mucha frecuencia en la radio. Conozco a dos que son de los que miran y de los cagones. En una película de Woody Allen, el personaje interpretado por él mismo asiste quieto y a oscuras (reflexión) en un cine a la proyección de una película en la que aparece Humphrey DeForest Bogart "Bogie" desfaciendo algun entuerto imagino, con tías buenas de por medio (acción). La melodía es pegadiza y tengo la sensación de haberla escuchado (en variaciones) un millón de veces. ¿Quieres decir que las mujeres heterosexuales seguidoras de Britney son una minoría dentro de su grupo de fanáticos? A mi no me pone y no me interesa su música. El principio básico de la estadística dice que correlación no implica causalidad. Tengo dos imágenes de BS en la cabeza: con la cabeza rapada y mirada perdida (se le fue la pinza con su agente, su hijo o su marido); con el chumino calvo, sin bragas y bajando de un vehículo motorizado. La metafotografía, ¿no existira una foto con la postura del fotógrafo disparando esta segunda instantánea?

Joder joder los Jonas Brothers, lo que me haces padecer. ¿Por desgraciar a una niña entiendes himen perforado por glande humano? Ojo al dato los Jonas Brothers sienten a veces oscuridad. Demostrado, un artista solo crea cuando sufre. Hacer arte consiste en lamerse las heridas. Uno de ellos calza unas patillas admirables, ¿serán de quita y pon como todo lo demás?

Eternamente joven

By Troy on February 10, 2009 11:13 PM | 1 Comment

Como dije antes, toda decisión adoptada por la embarazada me parece válida. Estoy bastante persuadido de que nunca me voy a ver en el papel de preñada; fundamentalmente porque meo de pie sin apenas dificultad.

La contrariedad de la pena de muerte es determinar el sujeto decisor. ¿Una persona con autoridad y potestad para juzgar y sentenciar conforme a preceptos dictados por la autoridad con atribuciones legitimadoras, en que se manda algo en consonancia con la justicia y para el bien de los gobernados? Me vale siempre que los gobernados hayan ejercido su poder por medio de representantes elegidos por sufragio universal. Estoy bastante persuadido de que nunca me voy a ver en el papel de juez; fundamentalmente por falta de vocación y formación.

No hay decisión colectiva directa, aparece como resultado indirecto de un conjunto de decisiones individuales directas. La cuestión de verdad es el ámbito de decisión de cada individuo y cómo sus propias decisiones individuales y las de sus congéneres lo modifican, aumentándolo o reduciéndolo. Tú, en tu manía igualitaria, desearás una sociedad en la que todos sus miembros tengan ámbitos de decision muy similares; yo deseo no predeterminar la nube de ámbitos de decisión sino que las series de decisiones individuales resulten en lo que sea. Tú fijas desde la teoría de una persona (tú) el resultado final, yo dejo desde la práctica de todas las personas un resultado final indeterminado de antemano y cambiante según cambien las contribuciones de los individuos. Tú apuestas por tu fósil y yo apuesto por un organismo vivo multipropiedad y eternamente joven.

La propiedad nunca está ni mal ni bien repartida; es válida siempre que haya salido naturalmente de decisiones individuales. No vale decir que se quiere algo, hay que tomar decisiones individuales que lleven a ese algo, conociendo la existencia de otras muchas decisiones individuales ajenas que pueden sumar o restar en esa dirección.

La ilusión del sexo

By Ludwig on February 10, 2009 4:50 PM | 5 Comments

Cada tarde, cuando ponen anuncios entre los dos episodios de los Simpson, me cambio a alguna de las cadenas musicales. Ayer vi "Circus" de Britney Spears y "When you look me in the eyes" de Jonas Brothers.

Dicen en el marketing que hay que vender con ilusión y comprar con desdén. La ilusión que nos quieren vender en el vídeo de Britney es, por enésima vez, follar con Britney Spears. Cada vídeo es un nuevo reempaquetado del producto, cada vez más explícito. Da una cierta sensación de que se están quedando sin ideas: todo, incluso elefantes, con tal de borrarnos de la cabeza el poco sex-appeal de su baile en los Grammys.

Jonas Brothers me hicieron mucha gracia, en el sentido de reírme, porque son una boy band que hace como que son los Strokes -- incluso un poco Thursday. [ La ostia, al final del vídeo en YouTube ponen un número de teléfono para llamarles!! ]

Ya que la música no tiene mucho interés, lo que se me ocurrió es mirar al público, que son casi todo chicas muy jóvenes. Pensando mal como es mi costumbre, me di cuenta de que estas bandas son aceptables para los padres (me refiero a los hombres, que son probablemente los que las llevan y las recogen) porque son unos eunucos, a los que se puede confiar a las niñas porque no van a hacerles nada. Son los padres aquí los que compran una entrada al mundo adulto, pero la compran con desdén, administrándola con cuentagotas, no vaya a ser que a la niña nos la desgracien. Las que ponen la ilusión son las chicas, que suelen seguir a estas bandas con un fervor que deja muy atrás a los metaleros (ejemplo de fidelidad a muerte del público). La ilusión que ponen es que realmente las dejen salir al mundo adulto de una vez, donde hay hombres que no son papá.

Los fetos me aburren

By Ludwig on February 9, 2009 4:00 PM | 5 Comments

Qué discusión más aburrida y propia de la clase de Ética del Instituto: ¿a partir de qué momento es un feto un ser humano? En disputada competición con la pregunta: ¿está justificada la pena de muerte?

Te responderé que a) me importa tres puñetas y b) los que responden que maten a unos (fetos) suelen responder que no maten a los otros (presos). Esto también es un lugar común, así que toda la discusión me aburre.

Sobre Warren Buffett: yo también alabo la decisión individual, y no creo que deba contraponerse a la decisión colectiva. Porque la decisión colectiva es una suma de decisiones individuales. ¿Cómo podría la parte ser algo distinto del todo? Otra pregunta clásica.

Pero hay una opción que no estás tomando en cuenta, que estás (ajajá) escamoteando como un tahúr: ¿qué pasa si otras personas, en uso de su libertad individual, deciden que WB tiene demasiado dinero, como él mismo, en su modestia, parece sugerir? ¿y si deciden aligerarle de su exceso de renta, a base del conocido método de ponerle un pistolón en la cara?

Me dirás: "es que eso no es una decisión individual, porque estás decidiendo sobre la propiedad de otro". Lo cual sólo indica que la cuestión de verdad es la propiedad, no la libertad, que a todos se reconoce sin problema -- siempre que no me toquen lo que es mío.

Me dirás: "pues que el señor Buffett se pague de su bolsillo un servicio de seguridad 24 horas." Cierto, pero llevando al extremo ese argumento, eso es precisamente lo que tenemos ahora: un servicio de seguridad 24/7 llamado policía y juzgados, cuya misión fundamental es dar seguridad jurídica a los que poseen, frente a los que quieren quitárselo.

En tu mundo de decisores atómicos, la individualidad se extiende hasta donde es contrarrestada por otra individualidad. Resulta muy bonito, pero no logra capturar la realidad por completo. En especial, falla cuando la propiedad está mal repartida, y según tú, hay que confiar en que "la mayoría de las personas quieran una sociedad más equitativa".

Para la economía, la mayoría de las personas no son el grupo numéricamente mayor de personas, sino el grupo de personas con una mayor renta. La voluntad de una mayoría de campesinos desheredados de un nuevo reparto de las tierras fértiles no vale nada frente a la voluntad de una minoría propietaria. Si esto fuera realmente así, el juego acabaría siempre con la victoria de los mismos. Que esto no sea siempre así quiere decir que hay algo que tu modelo, al que llamaré "de los gases libres" (porque además apesta), no está tomando en cuenta.

Y me he dejado algo en el tintero: tu frase de que "cualquier nivel de equidad es perfecto y será válido en todo momento" no es más que una reedición de Hegel, "lo que es racional existe, y lo que existe es racional". Qué cómodo, ¿no?

Vulgo chorba

By Troy on February 7, 2009 12:00 AM | No Comments

Mi ateismo me lleva a negar la existencia de una realidad objetiva, eterna, inmutable...porque de no ser así, habría que llamarla dios. Hay tantas realidades como sujetos decidiendo, y todas éstas son válidas. La razón no debe emplearse en distinguir la bondad o maldad de un asunto, sino determinar quien debe ser el sujeto decisor.

Yo no entro (porque no hay nada detrás) en si la interrupción deliberadamente provocada del embarazo es admisible o reprobable moralmente. En lo que sí entro y opino es en que la decisión de continuar o no con la gestación corresponde exclusivamente al ser preñado (vulgo chorba). Si decide seguir hasta el parto, bien; si decide cortar continuidad, bien también.

WB debe decidir por él solo, no por todos los miembros de la sociedad. Si él considera que ha recibido de la sociedad más de lo que ha dado, que haga sus cálculos y devuelva la diferencia como mejor le parezca. Esto me parece bien porque es WB el que decide (no el estado). Del mismo modo me parecería bien que WB estimara que está en equilibrio con la sociedad y decidiera actuar en consecuencia.

Este sistema, partidario de la libertad individual y social en lo político y de la iniciativa privada en lo económico, evita que la opinión de unos se imponga sobre todos. En él conviven opiniones opuestas.

La sociedad resultante bajo este sistema será tanto más equitativa (menores diferencias entre sus miembros) cuanto más individuos así lo quieran (tomando decisiones en esa dirección). El nivel predeterminado perfecto o ideal de equidad de la sociedad no existe o es cualquiera, siempre y cuando sea fruto de un conjunto de decisiones individuales; e irá cambiando en el tiempo y será valido en todo momento.

Egoísmo ilustrado

By Ludwig on February 6, 2009 6:03 PM | 2 Comments

Warren Buffett parece una buena persona y tiene razón en aceptar que su contribución a la sociedad no puede ser proporcional a sus enormes ingresos. Una buena parte se debe al azar, y otra parte a la contribución indirecta de otras personas.

Lo que no me entra en la cabeza es que de esto deduzcas que es mejor dejar que cada oveja busque salvar su culo. Precisamente, Buffett está dando argumentos para el socialismo: dado que el mercado no es capaz de reconocer quién es el que contribuye verdaderamente al bien de la sociedad, sino que sigue modas irracionales, es más eficiente repartir al menos una parte de la riqueza originada entre toda la sociedad. Y si me preguntas que por qué pienso que el mercado ha reconocido demasiado la labor de Buffett, te responderé que estamos discutiendo sus desinteresadas opiniones, pero no tenemos ni idea de las de sus "compañeros de buen ánimo y talento". Quizá ellos también hubieran tenido una opinión que compartir.

El reparto de la renta entre todos los actores sociales sigue el mismo argumento por el que es más eficiente dar cobertura sanitaria mínima a los que no pueden pagarla: porque evita que sean un cultivo de enfermedades para la población que sí puede pagarse la atención médica.

Pero se ve que por proponer un reparto más equitativo (que no igualitario), soy parte de una minoría "privilegiada e iluminada", que quiere imponerle a la mayoría cuánto deben ganar a través del Estado. En absoluto. Precisamente pienso que es el Estado el garante de que la distribución siga siendo la que es, como se ha podido ver en la reciente crisis financiera.

Eres tú precisamente el que se expresa supuestamente en nombre de la mayoría, cuyos intereses ya has decidido de antemano: deben ser egoístas, porque todo lo demás es "vanitas vanitatum" de unos cuantos vanguardistas. Y tú mismo adoptas el papel de egoísta ilustrado: todo el pueblo cada uno por sí mismo, pero por favor que no molesten con sus opiniones.

El cultivo del culo propio

By Troy on February 6, 2009 2:29 PM | 1 Comment

Warren Buffett (desconfía de quien no escriba la doble t) tira también de tu cuerda. Nunca en mi vida tuve un ídolo hasta saber de él; y esto fue hace muy poco. ¿Tienen los solipsistas menos ídolos, si alguno, que los miembros de la población general? Me permito traducir sus (WB) palabras: "Soy extraordinariamente afortunado. Nací en Estados Unidos; tuve unos padres fantásticos que se aseguraron de que mi formación fuera buena; he disfrutado de una familia maravillosa y excelente salud; vine equipado con un gen para los negocios que me permite prosperar de un modo altamente desproporcionado si lo comparamos con el de otras personas que contribuyen tanto o más que yo al bienestar de nuestra sociedad. Además, desde hace mucho, he tenido un empleo que amo y en el que me ayudan todos los días de innumerables maneras compañeros de buen ánimo y talento. No sorprende que vaya al trabajo gorjeando de júbilo." En más de una ocasión ha afirmado que la mayor parte de su éxito se debe a factores ajenos a su voluntad.

Si todas las ovejas nos preocupamos individualmete de que no se nos pele el culo de frío, los culos de todas las ovejas mejoran (como consecuencia indirecta) más que si una nomenclatura minoritaria, iluminada, vanguardista y, por supuesto, progresista (en su acepción bastarda) se preocupa y decide no sólo de sus minoritarios culos sino de los culos de todos e impide el cultivo del culo propio de una mayoria.

El rebaño y la ciudad

By Ludwig on February 5, 2009 5:06 PM | 2 Comments

La imagen que últimamente tengo en la cabeza cuando pienso en la sociedad es un rebaño de ovejas que se protege por la noche del frío formando un círculo. Todas las ovejas van buscando un hueco por el que entrar más adentro, y que se pele el culo de frío otra. La posibilidad de entrar más adentro no depende tanto de las dotes o el servicio a la comunidad de la oveja, sino del azar de que se forme un hueco, y de la rapidez para aprovecharlo. Porque en realidad todo el objetivo de la sociedad es no pasar frío, de manera que, con estar juntos, es suficiente. No hay nada que recompensar, y las ovejas que llegan más alto no tienen mayor sabiduría: simplemente, caen bien y han sabido aprovechar todos los huecos. En el centro del rebaño, aunque se esté calentito, no hay tampoco nada. Sólo un montón de mierda.

Esta dinámica gravitacional de los seres humanos es la que nos lleva a formar ciudades. En el centro de la ciudad tiene que haber algo que haya comenzado a atraer a la gente: una corte, un puerto, un puente... Una vez iniciado el proceso, puede convertirse en autosostenido, como la combustión de una estrella: mucha gente va a una ciudad porque allí hay trabajo, y hay trabajo porque allí vive mucha gente. El producto de la combustión de una estrella son los elementos "pesados", es decir, todos menos hidrógeno y helio. El producto de la "combustión" de una ciudad es el avance científico y cultural. Concretamente, aparecen individuos y comportamientos que una sociedad rural no puede permitirse, porque no son inmediatamente productivos. Sin embargo, es la ciudad la que alimenta al campo, porque es a través de la nueva tecnología como se puede aumentar la producción y aliviar el trabajo. (El ejemplo perfecto es el arado romano y el arado moderno. Durante mil años en Europa se usó un arado inútil para latitudes no mediterráneas. Nadie lo mejoró hasta que no se desarrollaron las ciudades del Norte.)

¿Pueden modelarse estos procesos? ¿Podremos calcular, aunque sea de manera estadística, cuál es la temperatura del proceso social? ¿Podemos estimar la frecuencia entre crisis, dado un conocimiento suficiente de la situación económica actual? ¿Puede todo ello resumirse en una sola variable: la densidad de población? ¿Es la moda, con toda su irracionalidad, la causa del comportamiento caótico en la economía?

Toda la vida es lucha

By Ludwig on February 4, 2009 5:46 PM | No Comments

Me recuerdas a la introducción de La Celestina: "Todas las cosas son criadas a manera de contienda o batalla. (...) Pues entre los animales ningún género carece de guerra: pesces, fieras, aues, serpientes, de lo qual todo, vna especie a otra persigue."

¿Soy yo un idealista? Eres tú el que no se da cuenta de que Cataluña lleva, desde hace 150 años, ganando la "guerra económica" y empatando -al menos- la "guerra cultural", como dices con lenguaje curiosamente soviético. Por eso estamos donde estamos, nos ha jodido Mayo con las flores. Si los catalanes fueran uno de esos pueblos en taparrabos que nos encontramos en Centroamérica, haría tiempo que serían una curiosidad etnográfica.

Yo no pienso que toda la vida sea lucha, porque es mucho peor: toda la vida es mamoneo. Tú le cubres el culo a ése de allá, ése te lo cubre a ti, mi amiguete sabe de un tema, tu amiguete es concejal de urbanismo... y al que se salga de la cola para recibir la manduca, le hacemos entrar en razón a estacazos.

Es un modelado de la sociedad que tiene la ventaja de describir tanto la colaboración como la competencia entre individuos: hoy por ti, mañana por mí, siempre y cuando seamos parte del mismo circuito social. Una especie va detrás de la otra, y nosotros somos los que corremos en círculo, persiguiéndonos a nosotros mismos.

Eso, la oscuridad y sus tetas.

By Troy on February 2, 2009 10:20 PM | 1 Comment

Yo quiero ser un ciudadano del mundo y de mi época. Quiero que mi lugar de nacimiento y las circunstancias materiales y espirituales de mis primeros años de vida influyan elástica y no plásticamente en mi paso por el mundo. Quiero buscar y ejercer universales. Quiero aprovechar todas las ventajas que el grado de progreso humano de mi época ofrece. Deseo que cuanto antes la nave espacial planeta tierra sea un solo país donde la misma legislación dé los mismos derechos y deberes a todos los hombres.

Los idealistas suelen olvidar que existe algo llamado "realidad" (cuyo ser es independiente de lo que haya dentro de su cabeza) y algo llamado "pasado" (que confiere al presente solidez e inercias que dificultan su cambio instantáneo y absoluto). Cataluña forma parte de España porque no ha ganado una puta guerra en su puta vida y la realidad la modelan los que ganan guerras. Entiéndase por guerra no sólo las armadas, sino también las morales, económicas, políticas, culturales, sociales... Nacionalismo y progresismo (en su acepción no bastarda) son términos contradictorios. Un nacionalista catalán es aquel que quiere ventajas exclusivas y especiales para los catalanes frente al resto de españoles. Un nacionalista español es aquel que quiere ventajas exclusivas y especiales para los españoles frente al resto de europeos. El nacionalismo beneficia fundamentalmente a la clase política (creando más burocracia y más empleos para políticos, familiars y amigos) y a la clase económica (generando proteccionismo para que el local que está subido a la burra no sea desbancado por un foráneo más competitivo).

La frase "Son españoles... los que no pueden ser otra cosa", atribuida a Antonio Cánovas del Castillo (en 1876 cuando se debatía en el Congreso el proyecto de Constitución) por José María Iribarren, en "El porqué de los dichos" (1955), en la página 238 (internet es maravilloso), me parece una soplapollez de proporciones bíblicas.

Aclarar que soy ateo. Cien millones de moscas no pueden estar equivocadas. ¡Come mierda! Vivo en Inglaterra y la bazofia bardenopenelopiana la estrenan aquí el 6 de febrero próximo. Frecuento bastante el cine por aquí. Cuando proyectan el trailer del coso, siento una terrible vergüenza, pero me calmo al pensar que el resto de personas en la sala (salvo quizá mi pechugona acompañante) desconocen mi nacionalidad. Eso, la oscuridad y sus tetas.

España sí o España no

By Ludwig on February 2, 2009 2:30 PM | 1 Comment

Vamos a por la otra bestia negra de los españoles que en el mundo han sido: ¿qué es España?

La pregunta es el origen de otras muchas, más relacionadas con la actualidad política: ¿quiénes son los españoles y en qué se diferencian de las personas que no son españolas? ¿cómo es posible que ésos de allá duden siquiera de que son españoles? ¿cómo es posible que ésos (de Madrid) no admitan de una vez que __<inserte reino medieval aquí>__ fue anexionada por la fuerza, muy en contra de su voluntad, y por tanto no es España? ¿por qué tengo yo que colaborar, léase pagar impuestos, en una sociedad que a lo mejor sí y a lo mejor no es la mía?

Se trata, como vemos sobre todo por la primera sub-pregunta, de una cuestión de identidad colectiva: a qué concepto de sí mismos deben lealtad un conjunto de personas.

Siguiendo la costumbre de dar soluciones tajantes en una sola frase, que inauguré en el primer post, voy a decir que: una identidad colectiva existe en tanto que otros colectivos entienden frases con sentido sobre ella, y tiene el mismo rango que los otros colectivos que la reconocen.

Por eso, cuando alguien enuncia la frase "soy de Jprguaw", para él mismo puede tener perfecto sentido, pero para nadie más; cuando dice "soy riojano", tiene sentido y se entiende dentro de España, pero probablemente no en el extranjero, por eso es una región de España; cuando dice "soy vasco", alguna gente fuera de España sabe de qué está hablando y otra no; mientras que si dice "soy español", probablemente en el extranjero sí entenderán a qué se refiere.

Así, "vasco" se queda en una mezcla de nacionalidad y región, dependiendo del oyente, y por eso el mayor esfuerzo de Cataluña y el País Vasco es encontrar el reconocimiento al nivel internacional. Y el mayor esfuerzo del centralismo español es que no lo consigan.

Lo interesante es que la identidad colectiva no depende de nada que haga o sea la persona concreta que nos ocupa; la identidad colectiva existe sólo en tanto que otras personas la reconozcan.

El problema de España es que España se ha cargado su propia identidad colectiva central, que es Castilla. Como Castilla se ha disuelto en España, sólo los castellanos no pueden definirse en ninguna parte más que como españoles. La prueba es que los andaluces, o gallegos, o canarios que viven en Cataluña no tienen problema en definirse como tales, pero no hay "emigrantes castellanos que viven en Cataluña".

Esta disolución de Castilla en España es entendida como un gesto de altruismo por los castellanos y como un expansionismo imperialista por los demás. En realidad no es puramente ninguna de las dos cosas, porque el proceso paralelo a esa expansión política ha sido el derrumbe económico de la sociedad castellana. España son los restos de la implosión de Castilla: una periferia desconectada de un centro reducido a una sola ciudad.

Si España quiere ser un país en el que se reconozcan catalanes, vascos y gallegos, entonces debe ofrecerles un nivel de reconocimiento en el que encajen. La pieza que está faltando es Castilla, como nacionalidad de igual rango que la catalana o la vasca.

Mientras siga faltando, el país sufrirá de la neurosis que ya conocemos. Todos sabemos que España es Castilla expandida, pero nunca lo decimos. El Ejército español, por ejemplo, tiene una estatua del Cid en su cuartel general, y en el pedestal lista sus victorias, empezando por Covadonga y siguiendo por todas las victorias castellanas en la Edad Media, cuando ni siquiera existía el Estado llamado España. Este cuartel general se encuentra en la calle principal de Madrid, que se llama "La Castellana". El segundo equipo del Real Madrid se llama "Castilla". Pero nunca se oye hablar de Castilla por la televisión, incluso produce una cierta vergüenza hablar de ella para no ser identificado como un extremista o un lunático.

La definición famosa de español es "el que no puede ser otra cosa". La frase se ha entendido a la izquierda como aquél que no tiene otro remedio, porque es pobre y preferiría apuntarse a un país rico, y a la derecha como aquél que tiene un destino importante y no reniega de él.

A lo mejor, inconscientemente, la frase significa que hay "otra cosa" que es lo que realmente somos pero no nos permitimos o no nos permiten ser. ¿Qué es esa otra cosa que los españoles eran y ya no son? ¿Qué es esa otra cosa que los españoles quieren ser? Cuando respondamos honestamente, a lo mejor averiguamos qué es España.

« January 2009 | Main Index | Archives | March 2009 »